Now it is getting interesting

You still here? Glad to see people invested into this blog. This is my first time creating something meaningful in form of a blog post. So thank you for sticking around. Now that we got that away, lets dive into the vast ocean that is the Parser.

So, what exactly is a parser? Well since we discussed lexer in layman's terms, lets do the same for a parser. A parser is a program that takes in the syntax tokens generated by the lexer and outputs a syntax tree. It also handles all the syntax errors. Thats it. End of the post. Thank you for reading.

No, seriously. Thats everything that a parser does, but how it achieves the parse tree is the main topic for todays blog. So, the parser uses something called parsing algorithm to generate the parse tree from the given tokens. Remember the algorithms that you studied in your college. Yes, the same ones. The top downs and the bottom ups or whatever. I don't really care. I just want to write something that gives me a syntax tree correctly. So for this part, we are going to do something similar to what we did with the lexer. We will have a class that gives us ability to store all the tokens from lexer, peek them so that we can see what the next token holds and a function to actually create the parse tree.

So the basic structure can be something like:

class Parser {

    protected position: number = 0;
    protected tokens: Array<SyntaxToken> = [];
    protected errors: Array<string> = [];

    constructor (tokens: Array<SyntaxToken>) {
        this.tokens = tokens.filter(t => {
            return t.getKind() !== SyntaxKind.WhiteSpaceToken || t.getKind() !== SyntaxKind.BadToken;
        });
    }
    
    public parse(): SyntaxTree {
        // Code the parse method
    }
    
    public current(): SyntaxToken {
        return this.peek(0);
    }
    
    public peek(offset: number): SyntaxToken 
    {
       let index = this.position + offset;

        if (index >= this.tokens.length) {
            return this.tokens[this.tokens.length - 1];
        }
        return this.tokens[index];
    }
    
    private match = (kind: SyntaxKind) : SyntaxToken => {
        const current = this.current();
        if (current.getKind() === kind) {
            return this.next();
        }

        this.errors.push(`Error: Unexpected token <${current.getKind()}> at position: ${current.getPosition()}. Expected <${kind}>!`);

        // Fabricating a custom token because the tokens do not match!
        return new SyntaxToken(kind, this.current().getPosition(), null, null);
    }
    
    
}

What we expect from Parser

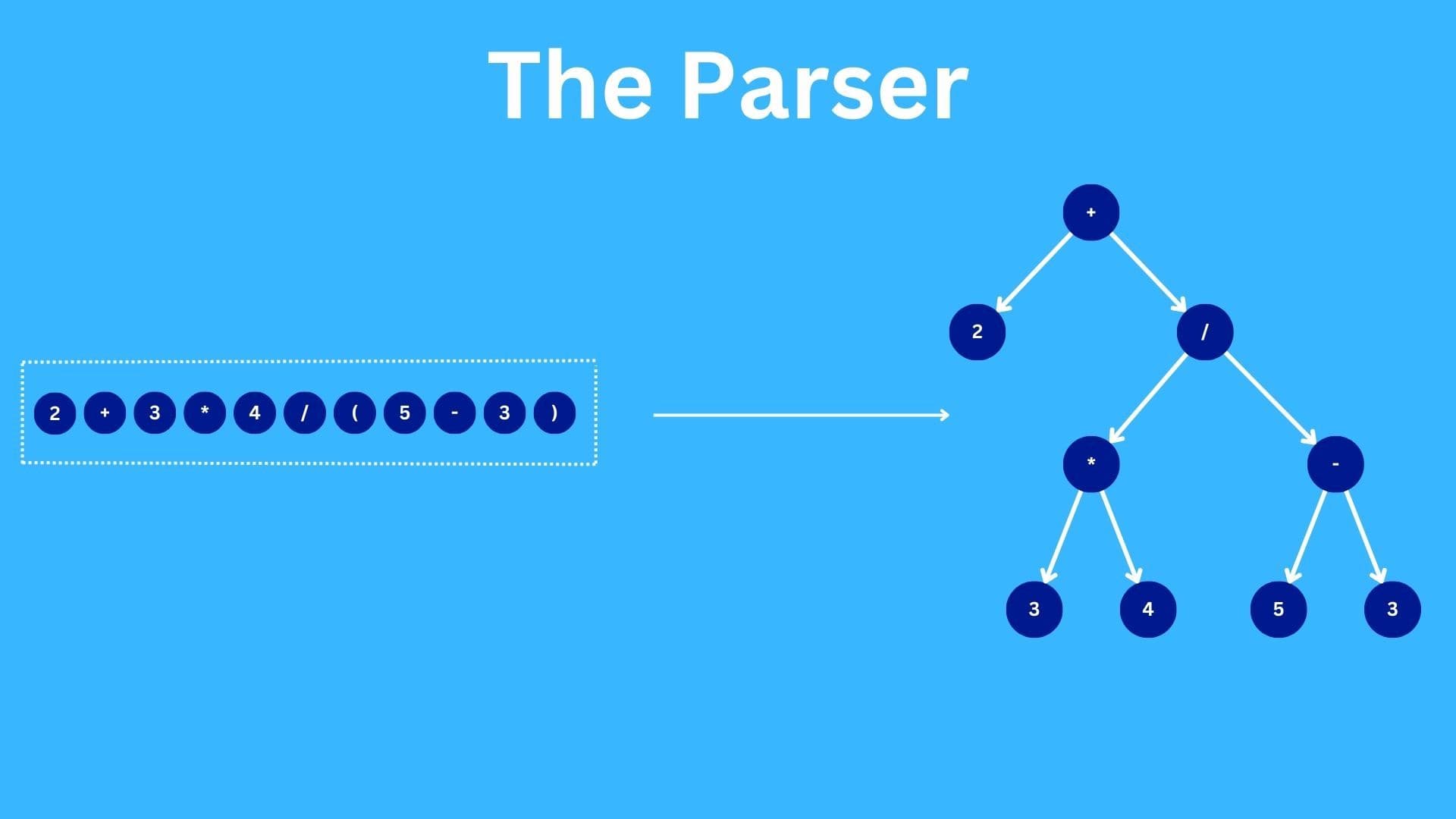
Let's say that we have an expression 1 + 2 * 3. Now, for this expression we want a tree representing these values in the following format.

// 1 + 2 * 3

     +
   /    \
 1       *
       /    \
     2      3

So, how are we going to get the tree from 1 + 2 * 3? This is where the Expression syntax kind that we discussed on the first post comes into play. As we discussed on the first and the second posts in this series, Expression Syntax kinds can have multiple other syntax kinds, operators and literal values as their children. In the above example, we can consider the whole tree to be a single binary expression of 1 on the left side, + as the operator and 2 * 3 on the right side. So, this is just an addition operation between 1 and 2 * 3. Upon further breakdown, we can see that the 2 * 3 is another binary expression; this time a multiplication between 2 and 3.

This is not the actual BinaryExpressionSyntax that is used in Balance, but we can get an idea on how it works from the following code.

new BinaryExpressionSyntax(
    new SyntaxNode(SyntaxKind.NumberToken, 1),
    new SyntaxNode(SyntaxKind.PlusToken, '+'),
    new BinaryExpressionSyntax(
         new SyntaxNode(SyntaxKind.NumberToken, 2),
         new SyntaxNode(SyntaxKind.MultiplyToken, '*'),
         new SyntaxNode(SyntaxKind.NumberToken, 3)
    )
)

You can already see where the tree structure is coming from.

But wait?

In the above example, we also can generate a parse tree which might look something like

// 1 + 2 * 3

              *
            /    \
         +      3
       /    \
     1      2

which would be problematic for us because this is not how mathematical computations are done. The above expression would result in the computation of 1 + 2 which is then multiplied with 3. Of course that is wrong and we don't want to do that. So, how do we avoid getting there? Well, it is kind of complicated. We will use something called a recursive descent parsing method to tackle this problem. What it essentially does is it breaks any expression down to two types, ie terms and factors. Terms represent the expressions that has lower priority than that of the factors. So, mathematically, we will be parsing anything that has / or * symbol in parseFactor method and anything that has + or - shall be parsed by parseTerm` method. Now, one more thing to consider is one method will be recursively calling another method as we will see in the example below:

private parseTerm(): ExpressionSyntax => {
    let left = this.parseFactor();
    while (this.current().getKind() === SyntaxKind.PlusToken || this.current().getKind() === SyntaxKind.MinusToken) {
        let operatorToken = this.next();
        let right = this.parseFactor();
        left = new BinaryExpressionSyntax(left, operatorToken, right)
    }

    return left;
}

private parseFactor(): ExpressionSyntax => {
    let left = this.parsePrimaryExpression();

    while (this.current().getKind() === SyntaxKind.AsteriskToken || this.current().getKind() === SyntaxKind.SlashToken) {
        let operatorToken = this.next();
        let right = this.parsePrimaryExpression();
        left = new BinaryExpressionSyntax(left, operatorToken, right)
    }

    return left;
}

private parsePrimaryExpression(): ExpressionSyntax => {
    if (this.current().getKind() === SyntaxKind.OpenParenthesisToken) {
        const left = this.next();
        const expression = this.parseTerm();
        const right = this.match(SyntaxKind.CloseParenthesisToken);
        return new ParenthesizedExpressionSyntax(left, expression, right);
    }
    
    const token = this.match(SyntaxKind.NumberToken);
    return new LiteralExpressionSyntax(token);
}

public parse(): SyntaxTree => {
    const expression = this.parseTerm();
    const eofToken = this.match(SyntaxKind.EndOfFileToken);
    return new SyntaxTree(this.errors, expression, eofToken);
}

What the hell is going on here 🤔

I know, it seems complicated with a lot of recursions going on. But we can see it works with the help of an example. Let's take an example of the string 2 + 3 * 4 / (5 - 3). When tokenized we get a sequence of tokens 2, +, 3, *, 4, /, (, 5, -, 5 and ). I have knowingly excluded all the white space tokens as they are of no significance when dealing with the parser.

Now, since parse is the only public method that can be called from outside of the Parser class, it is our entry point to the parser. We are assuming here that all the tokens generated by the lexer are filtered of white space tokens and are stored at tokens property of the Parser class.

In the parse method, the first thing we see is the const expression = this.parseTerm();. If we sequentially trace the function call, it will eventually lead to parsePrimaryExpression where for the first token, it returns a LiteralExpression with NumberToken as its child. Now, since we are calling the functions recursively, the while loop inside parseTerm is true as we are now dealing with the + symbol and it continues till we get something like this:

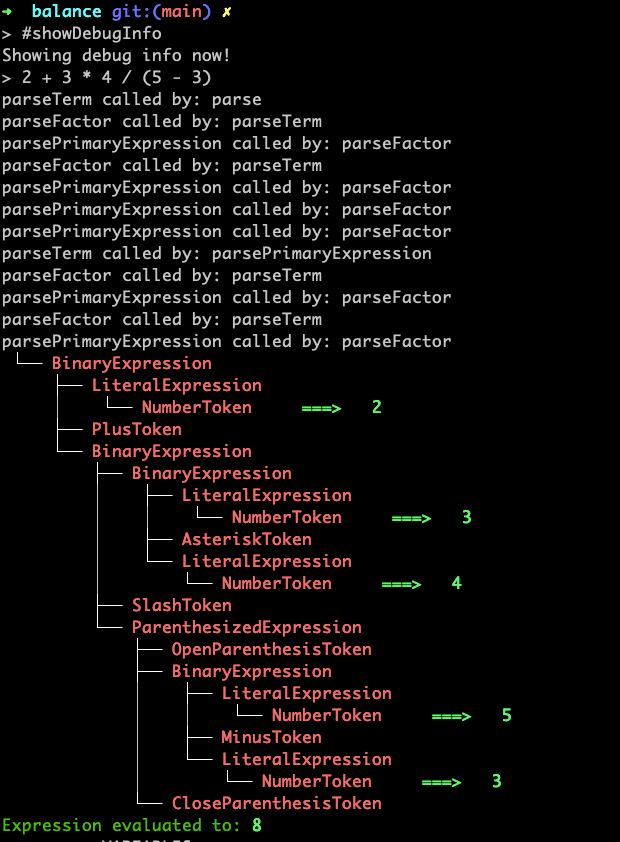
The main reason for this to work as we expect is that for any operator, parseFactor will always be called before parseTerm. This in turn results in multiplicative expressions being first processed before additive expressions, hence preserving the mathematical law.

Finally, the parse method wraps the result into a SyntaxTree object and returns the object. We will use this tree structure to generate the output.